Combined influence of shallowness and geometric imperfection on the buckling of clamped spherical shells
with Kanghyun Ki, Jeongrak Lee and Anna Lee


We investigate the combined influence of shallowness and geometric imperfection on the pressure-induced buckling behavior of clamped spherical shells. The buckling phenomenon in spherical shells has gained significant interest in diverse fields, such as soft robotics and biomechanics, due to its distinct and drastic shape morphing characteristics. However, a notable discrepancy between analytic solutions and experimental results persists, necessitating further research to comprehend the buckling behavior of spherical shells with varying shallowness and geometric imperfection. To address this gap, we experimentally investigate the buckling of clamped spherical shells under uniform pressure while controlling the shell shallowness over a wide range. The experimental results validate finite element simulations, enabling analysis of the variation in buckling pressure and behaviors by manipulating the shell shallowness and geometric imperfection. Our analysis reveals decaying oscillatory variations in the buckling strength versus the shallowness curves, eventually converging to stable buckling strength for sufficiently deep shells. Moreover, these curves exhibit changes in level and shape with varying geometric imperfection. We also observe non-axisymmetric buckling modes in shells with small geometric imperfection and specific shallowness ranges. Through parametric studies, we identify the geometric conditions influencing the buckling behavior, particularly the non-snap-through criteria and non-axisymmetric buckling modes. This comprehensive investigation sheds light on the interplay between shallowness and geometric imperfection affecting the buckling behavior of clamped spherical shells. The findings contribute to a deeper understanding of shell buckling phenomena and have implications for various shell design applications.
Related Publication:
Kanghyun Ki+, Jeongrak Lee+, and Anna Lee*, "Combined influence of shallowness and geometric imperfection on the buckling of clamped spherical shells," Journal of the Mechanics and Physics of Solids 185, 105554 (2024). [pdf]
Evolution of critical buckling conditions in imperfect bilayer shells through residual swelling
with Dong Yan, Matteo Pezzulla, Douglas P. Holmes, Pedro M. Reis

We propose and investigate a minimal mechanism that makes use of differential swelling to modify the critical buckling conditions of elastic bilayer shells, as measured by the knockdown factor. Our shells contain an engineered defect at the north pole and are made of two layers of different crosslinked polymers that exchange free molecular chains. Depending on the size of the defect and the extent of swelling, we can observe either a decreasing or increasing knockdown factor. FEM simulations are performed using a reduced model for the swelling process to aid us in rationalizing the underlying mechanism, providing a qualitative agreement with experiments. We believe that the working principle of our mechanism can be extended to bimetallic shells undergoing variations in temperature and to shells made of pH-responsive gels, where the change in knockdown factor could be changed dynamically.
Related Publication:
Anna Lee, Dong Yan, Matteo Pezzulla, Douglas P. Holmes, Pedro M. Reis*, "Evolution of critical buckling conditions in imperfect bilayer shells through residual swelling," Soft Matter 15 , 6134-6144 (2019). [pdf]
Buckling of a pressurized hemispherical shell subjected to a probing force
with Joel Marthelot, Francisco López-Jiménez, John W. Hutchinson, and Pedro M. Reis

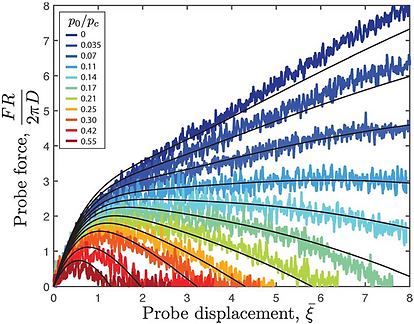
We study the buckling of hemispherical elastic shells subjected to the combined effect of pressure loading and a probing force. We perform an experimental investigation using thin shells of nearly uniform thickness that are fabricated with a well-controlled geometric imperfection. By systematically varying the indentation displacement and the geometry of the probe, we study the effect that the probe-induced deflections have on the buckling strength of our spherical shells. The experimental results are then compared to f inite element simulations, as well as to recent theoretical predictions from the literature. Inspired by a nondestructive technique that was recently proposed to evaluate the stability of elastic shells, we characterize the nonlinear load-deflection mechanical response of the probe for different values of the pressure loading. We demonstrate that this nondestructive method is a successful local way to assess the stability of spherical shells.
Related Publication:
Joel Marthelot, Francisco López-Jiménez, Anna Lee, John W. Hutchinson, and Pedro M. Reis*, “Buckling of a pressurized hemispherical shell subjected to a probing force,” Journal of Applied Mechanics 84, 121005 (2017). [pdf]
Critical buckling pressure of precisely imperfect shells
with Francisco López-Jiménez, Joel Marthelot, John W. Hutchinson, and Pedro M. Reis

We study the effect of a dimplelike geometric imperfection on the critical buckling load of spherical elastic shells under pressure loading. This investigation combines precision experiments, finite element modeling, and numerical solutions of a reduced shell theory, all of which are found to be in excellent quantitative agreement. In the experiments, the geometry and magnitude of the defect can be designed and precisely fabricated through a customizable rapid prototyping technique. Our primary focus is on predictively describing the imperfection sensitivity of the shell to provide a quantitative relation between its knockdown factor and the amplitude of the defect. In addition, we find that the buckling pressure becomes independent of the amplitude of the defect beyond a critical value. The level and onset of this plateau are quantified systematically and found to be affected by a single geometric parameter that depends on both the radius-to-thickness ratio of the shell and the angular width of the defect. To the best of our knowledge, this is the first time that experimental results on the knockdown factors of imperfect spherical shells have been accurately predicted, through both finite element modeling and shell theory solutions.
Related Publications:
Anna Lee, Francisco López-Jiménez, Joel Marthelot, John W. Hutchinson, and Pedro M. Reis*, “The geometric role of precisely engineered imperfections on the critical buckling load of spherical elastic shells,” Journal of Applied Mechanics 83, 111005 (2016). [pdf]
Francisco López-Jiménez, Joel Marthelot, Anna Lee, John W. Hutchinson, and Pedro M. Reis*, “Knockdown factor for the buckling of spherical shells containing large-amplitude geometric defects,” Journal of Applied Mechanics 84, 034501 (2017). [pdf]
